前言
在 Canvas 中對文本填充水平或垂直的線性漸變可以輕易實現,而帶角度的漸變就復雜很多;就好像下面這樣,假設文本矩形寬為 W, 高為 H, 左上角坐標為 X, Y。

猜想與答案
給出兩個答案:
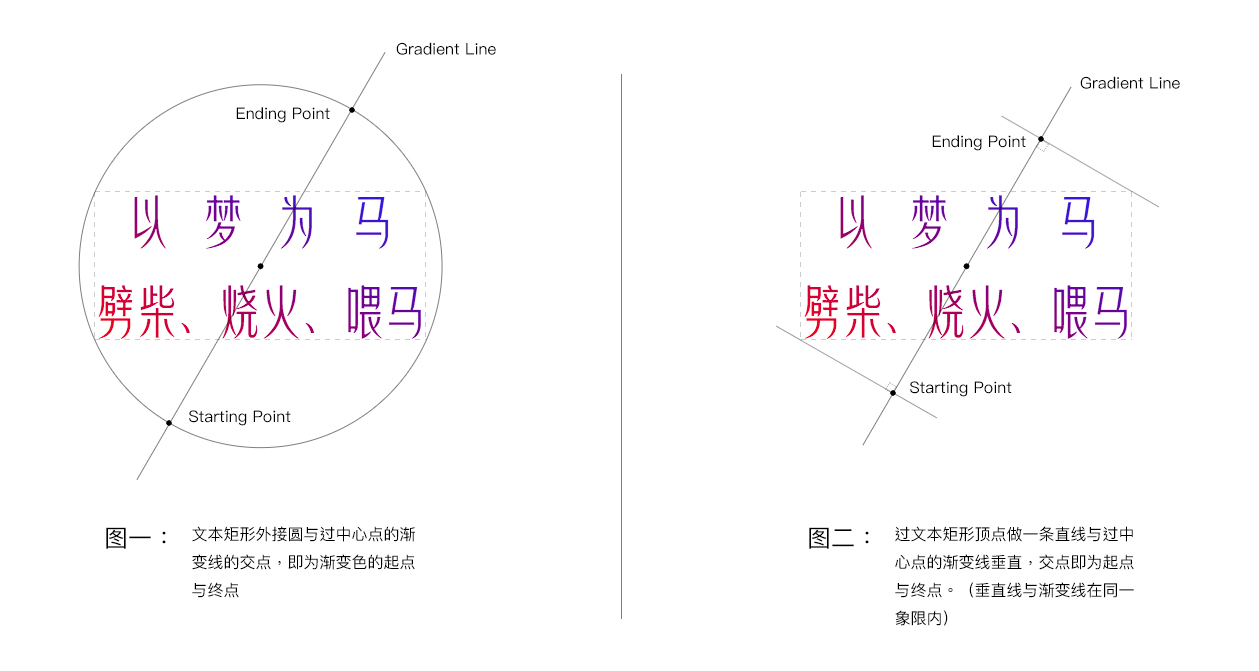
正確答案是圖二,因為這樣得出來的坐標生成的漸變最緊接文本矩形邊界,它的運動軌跡如下動圖:
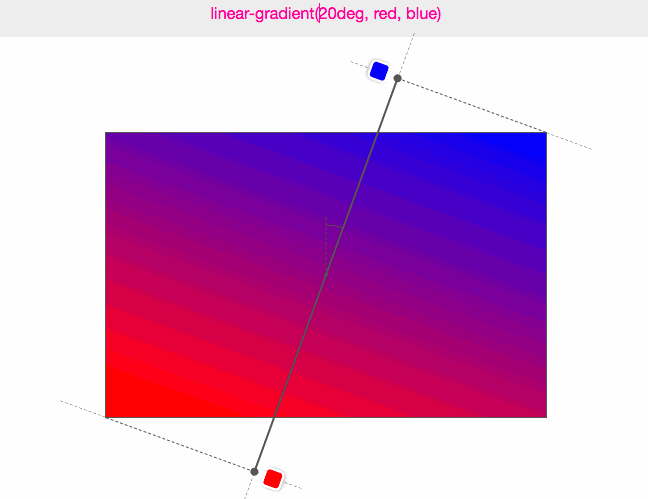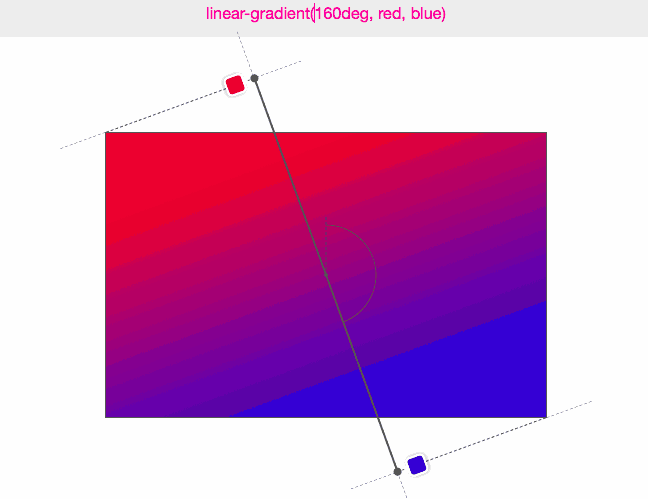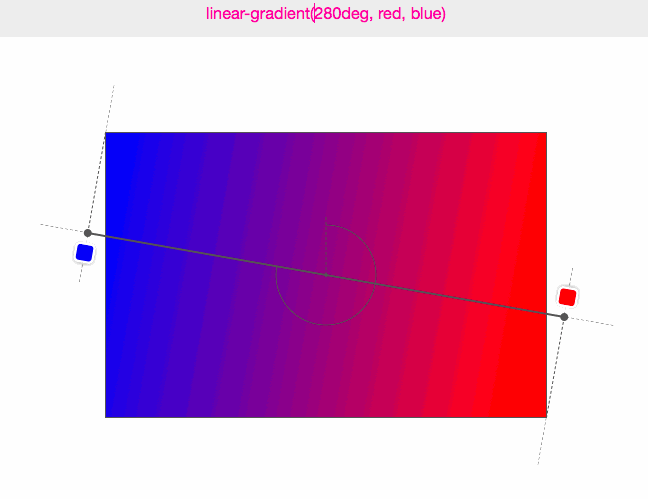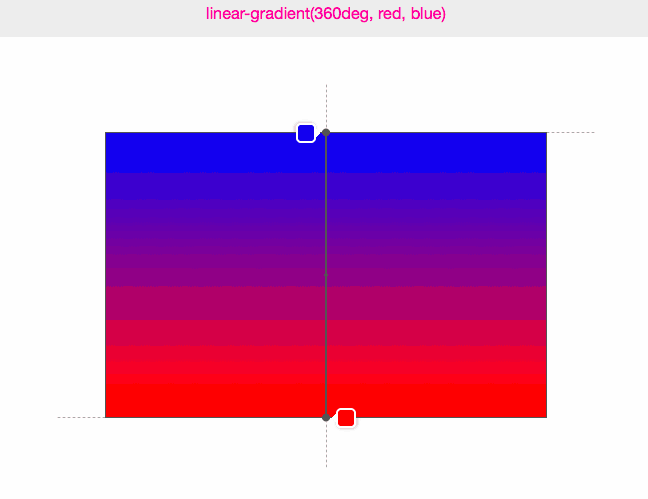
(圖來源:Do you really know CSS linear-gradients)
漸變起點與終點坐標的計算
所以,漸變的起點與終點坐標該怎么計算呢?答:
- 先求得起點與終點的長度(距離)。
- 根據長度與文本矩形的中心點坐標分別計算出起點與終點坐標。
線性漸變長度的計算 W3C 給出了一個公式(A 表示角度):
gradientLineLength = abs(W * sin(A)) + abs(H * cos(A))
不過,該公式主要應用于 CSS 的線性漸變設置,即以 12 點鐘方向為 0°,順時針旋轉。
而我們需要的是以 3 點鐘方向為 0°,逆時針旋轉,即公式為:
gradientLineLength = abs(W * cos(A)) + abs(H * sin(A))
// 半長:
halfGradientLineLength = (abs(W * cos(A)) + abs(H * sin(A))) / 2
那么這個公式是怎么來的呢?以下是筆者的求解:
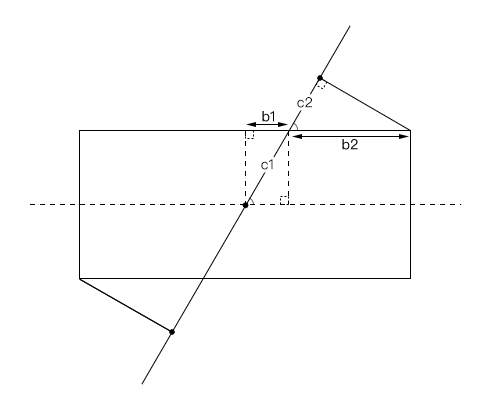
由圖可得以下方程組:
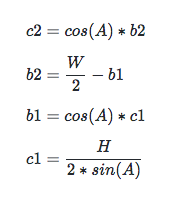
因此可推導出:
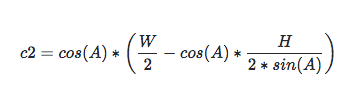
化簡后為:
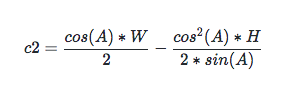
所以 c1 + c2 為:
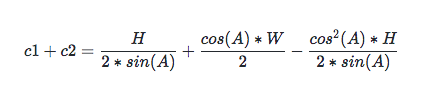
由三角函數平方公式知:cos(A) * cos(A) = 1 - sin(A) * sin(A), 代入 c1 + c2:
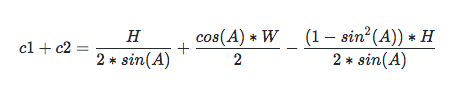
第一步化簡后:
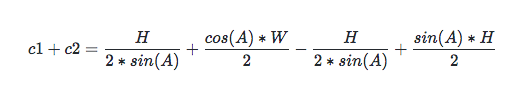
最后的結果就是:
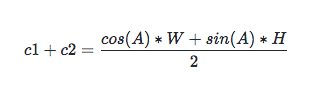
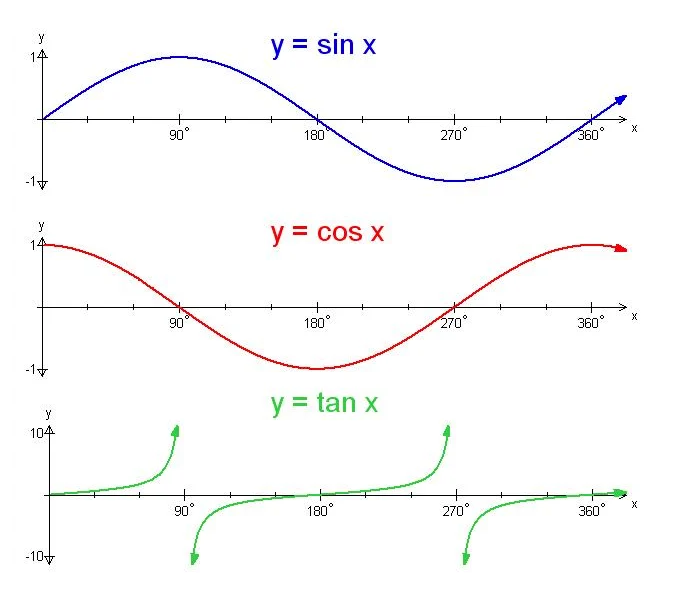
因為 sin, cos 在函數周期內存在負值(見下面角度對應的三角函數周期圖),所以線性漸變的長度需要取絕對值。
至此,我們知道了線性漸變長度,文本矩形的中心點坐標很好算,即:
centerX = X + W / 2
centerY = Y + H / 2
所以,起點與終點的坐標分別為:
startX = centerX - cos(A) * halfGradientLineLength
startY = centerY + sin(A) * halfGradientLineLength
endX = centerX + cos(A) * halfGradientLineLength
endY = centerY - sin(A) * halfGradientLineLength
看看最終效果
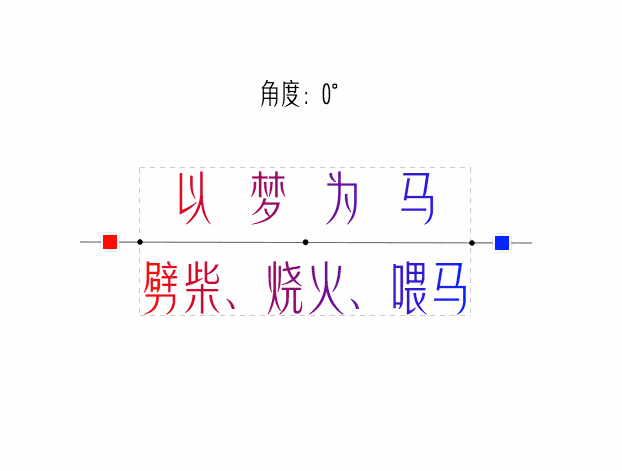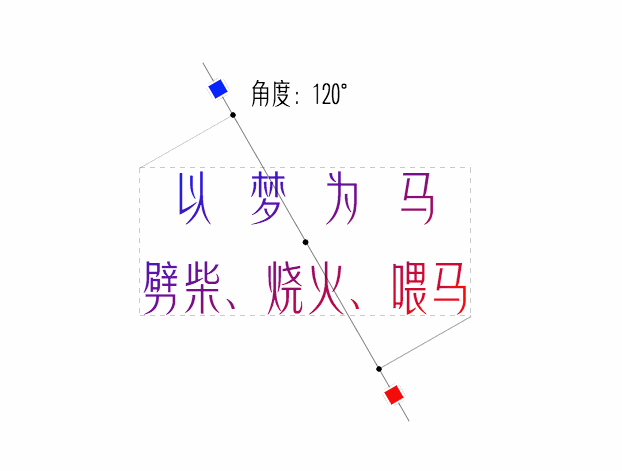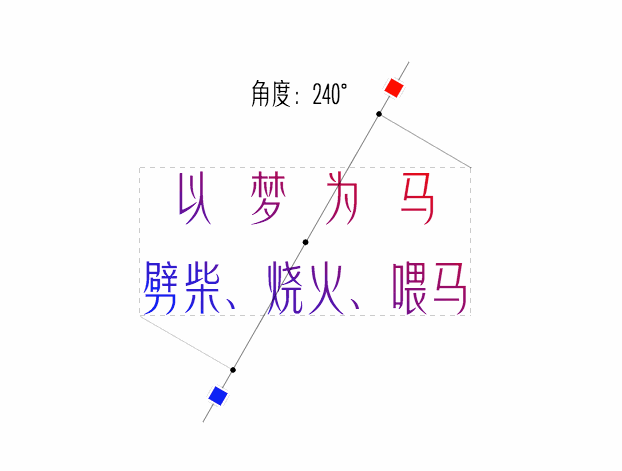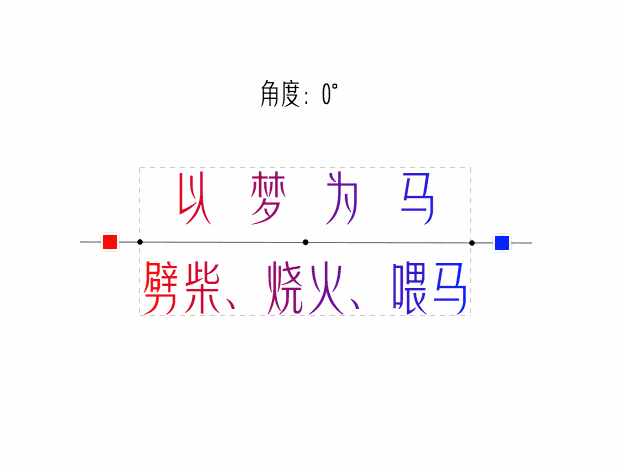
經驗注釋
進行三角函數計算時,應盡量避免先用 tan, 因為 tan 在其周期內存在無窮值,需要做特定的條件判斷,而 sin, cos 沒有此類問題,代碼書寫更為簡潔清晰并且不會因疏忽產生錯誤,見下面三角函數與角度的對應關系周期圖。
參閱
Do you really know CSS linear-gradients?
MDN linear-gradient
W3C - CSS Images Module Level 3 # linear-gradients
到此這篇關于Canvas 文本填充線性漸變的使用詳解的文章就介紹到這了,更多相關Canvas文本填充線性漸變內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章,希望大家以后多多支持腳本之家!