目錄
- 技術背景
- 打格點算法實現
- 打格點算法加速
- 總結概要
技術背景
在數學和物理學領域,總是充滿了各種連續的函數模型。而當我們用現代計算機的技術去處理這些問題的時候,事實上是無法直接處理連續模型的,絕大多數的情況下都要轉化成一個離散的模型再進行數值的計算。比如計算數值的積分,計算數值的二階導數(海森矩陣)等等。這里我們所介紹的打格點的算法,正是一種典型的離散化方法。這個對空間做離散化的方法,可以在很大程度上簡化運算量。比如在分子動力學模擬中,計算近鄰表的時候,如果不采用打格點的方法,那么就要針對整個空間所有的原子進行搜索,計算出來距離再判斷是否近鄰。而如果采用打格點的方法,我們只需要先遍歷一遍原子對齊進行打格點的離散化,之后再計算近鄰表的時候,只需要計算三維空間下鄰近的27個格子中的原子是否滿足近鄰條件即可。在這篇文章中,我們主要探討如何用GPU來實現打格點的算法。
打格點算法實現
我們先來用一個例子說明一下什么叫打格點。對于一個給定所有原子坐標的系統,也就是已知了[x,y,z],我們需要得到的是這些原子所在的對應的格子位置[nx,ny,nz]。我們先看一下在CPU上的實現方案,是一個遍歷一次的算法:
# cuda_grid.py
from numba import jit
from numba import cuda
import numpy as np
def grid_by_cpu(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
if __name__=='__main__':
np.random.seed(1)
atoms = 4
grid_size = 0.1
crd = np.random.random((atoms,3)).astype(np.float32)
xmin = min(crd[:,0])
ymin = min(crd[:,1])
zmin = min(crd[:,2])
xmax = max(crd[:,0])
ymax = max(crd[:,1])
zmax = max(crd[:,2])
xgrids = int((xmax-xmin)/grid_size)+1
ygrids = int((ymax-ymin)/grid_size)+1
zgrids = int((zmax-zmin)/grid_size)+1
rxyz = np.array([xmin,ymin,zmin,grid_size], dtype=np.float32)
grids = np.ones_like(crd)*(-1)
grids = grids.astype(np.float32)
grids_cpu = grid_by_cpu(crd, rxyz, atoms, grids)
print (crd)
print (grids_cpu)
import matplotlib.pyplot as plt
plt.figure()
plt.plot(crd[:,0], crd[:,1], 'o', color='red')
for grid in range(ygrids+1):
plt.plot([xmin,xmin+grid_size*xgrids], [ymin+grid_size*grid,ymin+grid_size*grid], color='black')
for grid in range(xgrids+1):
plt.plot([xmin+grid_size*grid,xmin+grid_size*grid], [ymin,ymin+grid_size*ygrids], color='black')
plt.savefig('Atom_Grids.png')
輸出結果如下,
$ python3 cuda_grid.py
[[4.17021990e-01 7.20324516e-01 1.14374816e-04]
[3.02332580e-01 1.46755889e-01 9.23385918e-02]
[1.86260208e-01 3.45560730e-01 3.96767467e-01]
[5.38816750e-01 4.19194520e-01 6.85219526e-01]]
[[2. 5. 0.]
[1. 0. 0.]
[0. 1. 3.]
[3. 2. 6.]]
上面兩個打印輸出就分別對應于[x,y,z]和[nx,ny,nz],比如第一個原子被放到了編號為[2,5,0]的格點。那么為了方便理解打格點的方法,我們把這個三維空間的原子系統和打格點以后的標號取前兩個維度來可視化一下結果,作圖以后效果如下:
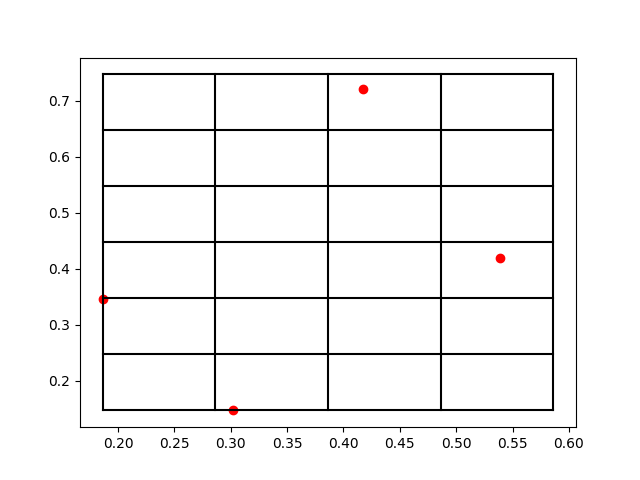
我們可以看到,這些紅色的點就是原子所處的位置,而黑色的網格線就是我們所標記的格點。在原子數量比較多的時候,有可能出現在一個網格中存在很多個原子的情況,所以如何打格點,格點大小如何去定義,這都是不同場景下的經驗參數,需要大家一起去摸索。
打格點算法加速
在上面這個算法實現中,我們主要是用到了一個for循環,這時候我們可以想到numba所支持的向量化運算,還有GPU硬件加速,這里我們先對比一下三種實現方案的計算結果:
# cuda_grid.py
from numba import jit
from numba import cuda
import numpy as np
def grid_by_cpu(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@jit
def grid_by_jit(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@cuda.jit
def grid_by_gpu(crd, rxyz, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
i,j = cuda.grid(2)
grids[i][j] = int((crd[i][j]-rxyz[j])/rxyz[3])
if __name__=='__main__':
np.random.seed(1)
atoms = 4
grid_size = 0.1
crd = np.random.random((atoms,3)).astype(np.float32)
xmin = min(crd[:,0])
ymin = min(crd[:,1])
zmin = min(crd[:,2])
xmax = max(crd[:,0])
ymax = max(crd[:,1])
zmax = max(crd[:,2])
xgrids = int((xmax-xmin)/grid_size)+1
ygrids = int((ymax-ymin)/grid_size)+1
zgrids = int((zmax-zmin)/grid_size)+1
rxyz = np.array([xmin,ymin,zmin,grid_size], dtype=np.float32)
crd_cuda = cuda.to_device(crd)
rxyz_cuda = cuda.to_device(rxyz)
grids = np.ones_like(crd)*(-1)
grids = grids.astype(np.float32)
grids_cpu = grid_by_cpu(crd, rxyz, atoms, grids)
grids = np.ones_like(crd)*(-1)
grids_jit = grid_by_jit(crd, rxyz, atoms, grids)
grids = np.ones_like(crd)*(-1)
grids_cuda = cuda.to_device(grids)
grid_by_gpu[(atoms,3),(1,1)](crd_cuda,
rxyz_cuda,
grids_cuda)
print (crd)
print (grids_cpu)
print (grids_jit)
print (grids_cuda.copy_to_host())
輸出結果如下:
$ python3 cuda_grid.py
/home/dechin/anaconda3/lib/python3.8/site-packages/numba/cuda/compiler.py:865: NumbaPerformanceWarning: Grid size (12) 2 * SM count (72) will likely result in GPU under utilization due to low occupancy.
warn(NumbaPerformanceWarning(msg))
[[4.17021990e-01 7.20324516e-01 1.14374816e-04]
[3.02332580e-01 1.46755889e-01 9.23385918e-02]
[1.86260208e-01 3.45560730e-01 3.96767467e-01]
[5.38816750e-01 4.19194520e-01 6.85219526e-01]]
[[2. 5. 0.]
[1. 0. 0.]
[0. 1. 3.]
[3. 2. 6.]]
[[2. 5. 0.]
[1. 0. 0.]
[0. 1. 3.]
[3. 2. 6.]]
[[2. 5. 0.]
[1. 0. 0.]
[0. 1. 3.]
[3. 2. 6.]]
我們先看到這里面的告警信息,因為GPU硬件加速要在一定密度的運算量之上才能夠有比較明顯的加速效果。比如說我們只是計算兩個數字的加和,那么是完全沒有必要使用到GPU的。但是如果我們要計算兩個非常大的數組的加和,那么這個時候GPU就能夠發揮出非常大的價值。因為這里我們的案例中只有4個原子,因此提示我們這時候是體現不出來GPU的加速效果的。我們僅僅關注下這里的運算結果,在不同體系下得到的格點結果是一致的,那么接下來就可以對比一下幾種不同實現方式的速度差異。
# cuda_grid.py
from numba import jit
from numba import cuda
import numpy as np
def grid_by_cpu(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@jit
def grid_by_jit(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@cuda.jit
def grid_by_gpu(crd, rxyz, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
i,j = cuda.grid(2)
grids[i][j] = int((crd[i][j]-rxyz[j])/rxyz[3])
if __name__=='__main__':
import time
from tqdm import trange
np.random.seed(1)
atoms = 100000
grid_size = 0.1
crd = np.random.random((atoms,3)).astype(np.float32)
xmin = min(crd[:,0])
ymin = min(crd[:,1])
zmin = min(crd[:,2])
xmax = max(crd[:,0])
ymax = max(crd[:,1])
zmax = max(crd[:,2])
xgrids = int((xmax-xmin)/grid_size)+1
ygrids = int((ymax-ymin)/grid_size)+1
zgrids = int((zmax-zmin)/grid_size)+1
rxyz = np.array([xmin,ymin,zmin,grid_size], dtype=np.float32)
crd_cuda = cuda.to_device(crd)
rxyz_cuda = cuda.to_device(rxyz)
cpu_time = 0
jit_time = 0
gpu_time = 0
for i in trange(100):
grids = np.ones_like(crd)*(-1)
grids = grids.astype(np.float32)
time0 = time.time()
grids_cpu = grid_by_cpu(crd, rxyz, atoms, grids)
time1 = time.time()
grids = np.ones_like(crd)*(-1)
time2 = time.time()
grids_jit = grid_by_jit(crd, rxyz, atoms, grids)
time3 = time.time()
grids = np.ones_like(crd)*(-1)
grids_cuda = cuda.to_device(grids)
time4 = time.time()
grid_by_gpu[(atoms,3),(1,1)](crd_cuda,
rxyz_cuda,
grids_cuda)
time5 = time.time()
if i != 0:
cpu_time += time1 - time0
jit_time += time3 - time2
gpu_time += time5 - time4
print ('The time cost of CPU calculation is: {}s'.format(cpu_time))
print ('The time cost of JIT calculation is: {}s'.format(jit_time))
print ('The time cost of GPU calculation is: {}s'.format(gpu_time))
輸出結果如下:
$ python3 cuda_grid.py
100%|███████████████████████████| 100/100 [00:2300:00, 4.18it/s]
The time cost of CPU calculation is: 23.01943016052246s
The time cost of JIT calculation is: 0.04810166358947754s
The time cost of GPU calculation is: 0.01806473731994629s
在100000個原子的體系規模下,普通的for循環實現效率就非常的低下,需要23s,而經過向量化運算的加速之后,直接飛升到了0.048s,而GPU上的加速更是達到了0.018s,相比于沒有GPU硬件加速的場景,實現了將近2倍的加速。但是這還遠遠不是GPU加速的上限,讓我們再測試一個更大的案例:
# cuda_grid.py
from numba import jit
from numba import cuda
import numpy as np
def grid_by_cpu(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@jit
def grid_by_jit(crd, rxyz, atoms, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
for i in range(atoms):
grids[i][0] = int((crd[i][0]-rxyz[0])/rxyz[3])
grids[i][1] = int((crd[i][1]-rxyz[1])/rxyz[3])
grids[i][2] = int((crd[i][2]-rxyz[2])/rxyz[3])
return grids
@cuda.jit
def grid_by_gpu(crd, rxyz, grids):
"""Transform coordinates [x,y,z] into grids [nx,ny,nz].
Args:
crd(list): The 3-D coordinates of atoms.
rxyz(list): The list includes xmin,ymin,zmin,grid_num.
atoms(int): The total number of atoms.
grids(list): The transformed grids matrix.
"""
i,j = cuda.grid(2)
grids[i][j] = int((crd[i][j]-rxyz[j])/rxyz[3])
if __name__=='__main__':
import time
from tqdm import trange
np.random.seed(1)
atoms = 5000000
grid_size = 0.1
crd = np.random.random((atoms,3)).astype(np.float32)
xmin = min(crd[:,0])
ymin = min(crd[:,1])
zmin = min(crd[:,2])
xmax = max(crd[:,0])
ymax = max(crd[:,1])
zmax = max(crd[:,2])
xgrids = int((xmax-xmin)/grid_size)+1
ygrids = int((ymax-ymin)/grid_size)+1
zgrids = int((zmax-zmin)/grid_size)+1
rxyz = np.array([xmin,ymin,zmin,grid_size], dtype=np.float32)
crd_cuda = cuda.to_device(crd)
rxyz_cuda = cuda.to_device(rxyz)
jit_time = 0
gpu_time = 0
for i in trange(100):
grids = np.ones_like(crd)*(-1)
time2 = time.time()
grids_jit = grid_by_jit(crd, rxyz, atoms, grids)
time3 = time.time()
grids = np.ones_like(crd)*(-1)
grids_cuda = cuda.to_device(grids)
time4 = time.time()
grid_by_gpu[(atoms,3),(1,1)](crd_cuda,
rxyz_cuda,
grids_cuda)
time5 = time.time()
if i != 0:
jit_time += time3 - time2
gpu_time += time5 - time4
print ('The time cost of JIT calculation is: {}s'.format(jit_time))
print ('The time cost of GPU calculation is: {}s'.format(gpu_time))
在這個5000000個原子的案例中,因為普通的for循環已經實在是跑不動了,因此我們就干脆不統計這一部分的時間,最后輸出結果如下:
$ python3 cuda_grid.py
100%|███████████████████████████| 100/100 [00:0900:00, 10.15it/s]
The time cost of JIT calculation is: 2.3743042945861816s
The time cost of GPU calculation is: 0.022843599319458008s
在如此大規模的運算下,GPU實現100倍的加速,而此時作為對比的CPU上的實現方法是已經用上了向量化運算的操作,也已經可以認為是一個極致的加速了。
總結概要
在這篇文章中,我們主要介紹了打格點算法在分子動力學模擬中的重要價值,以及幾種不同的實現方式。其中最普通的for循環的實現效率比較低下,從算法復雜度上來講卻已經是極致。而基于CPU上的向量化運算的技術,可以對計算過程進行非常深度的優化。當然,這個案例在不同的硬件上也能夠發揮出明顯不同的加速效果,在GPU的加持之下,可以獲得100倍以上的加速效果。這也是一個在Python上實現GPU加速算法的一個典型案例。
到此這篇關于Python3實現打格點算法的GPU加速的文章就介紹到這了,更多相關Python3實現打格點算法內容請搜索腳本之家以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持腳本之家!
您可能感興趣的文章:- Python3爬樓梯算法示例
- Python3 A*尋路算法實現方式
- Python3.0 實現決策樹算法的流程
- Python3實現的判斷環形鏈表算法示例