先前我們講的都是“線性結(jié)構(gòu)”，他的特征就是“一個(gè)節(jié)點(diǎn)最多有一個(gè)”前驅(qū)“和一個(gè)”后繼“。那么我們今天講的樹會(huì)是怎樣的呢？
我們可以對(duì)”線性結(jié)構(gòu)“改造一下，變?yōu)椤币粋€(gè)節(jié)點(diǎn)最多有一個(gè)"前驅(qū)“和”多個(gè)后繼“。哈哈，這就是我們今天說的”樹“。
一： 樹
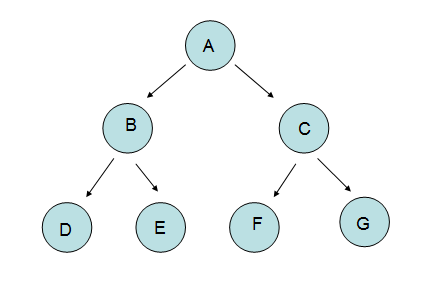
我們思維中的”樹“就是一種枝繁葉茂的形象，那么數(shù)據(jù)結(jié)構(gòu)中的”樹“該是怎么樣呢？對(duì)的，他是一種現(xiàn)實(shí)中倒立的樹。
1：術(shù)語
其實(shí)樹中有很多術(shù)語的，這個(gè)是我們學(xué)習(xí)樹形結(jié)構(gòu)必須掌握的。
1> 父節(jié)點(diǎn)，子節(jié)點(diǎn)，兄弟節(jié)點(diǎn)
這個(gè)就比較簡單了，B和C的父節(jié)點(diǎn)就是A，反過來說就是B和C是A的子節(jié)點(diǎn)。B和C就是兄弟節(jié)點(diǎn)。
2> 結(jié)點(diǎn)的度
其實(shí)”度“就是”分支數(shù)“，比如A的分支數(shù)有兩個(gè)“B和C",那么A的度為2。
3> 樹的度
看似比較莫名其妙吧，他和”結(jié)點(diǎn)的度“的區(qū)別就是，樹的度講究大局觀，乃樹中最大的結(jié)點(diǎn)度，其實(shí)也就是2。
4> 葉結(jié)點(diǎn)，分支結(jié)點(diǎn)
葉結(jié)點(diǎn)就是既沒有左孩子也沒有右孩子結(jié)點(diǎn)，也就是結(jié)點(diǎn)度為0。分支節(jié)點(diǎn)也就是if的else的條件咯。
5> 結(jié)點(diǎn)的層數(shù)
這個(gè)很簡單，也就是樹有幾層。
6> 有序樹，無序樹
有序樹我們先前也用過，比如“堆”和“二叉排序樹”，說明這種樹是按照一定的規(guī)則進(jìn)行排序的，else條件就是無序樹。
7> 森林
現(xiàn)實(shí)中，很多的樹形成了森林，那在數(shù)據(jù)結(jié)構(gòu)中，我們把上圖的“A”節(jié)點(diǎn)砍掉，那么B，C子樹合一起就是森林咯。
2: 樹的表示
樹這個(gè)結(jié)構(gòu)的表示其實(shí)有很多種，常用的也就是“括號(hào)”表示法。
比如上面的樹就可以表示為：(A(B(D),(E)),(C(F),(G)))
二： 二叉樹
在我們項(xiàng)目開發(fā)中，很多地方都會(huì)用到樹，但是多叉樹的處理還是比較糾結(jié)的，所以俺們本著“大事化小，小事化了“的原則
把”多叉樹“轉(zhuǎn)化為”二叉樹“，那么問題就簡化了很多。
1： ”二叉樹“和”樹“有什么差異呢？
第一點(diǎn): 樹的度沒有限制，而“二叉樹”最多只能有兩個(gè)，不然也就不叫二叉樹了，哈哈。
第二點(diǎn)：樹中的子樹沒有左右劃分，很簡單啊，找不到參照點(diǎn)，二叉樹就有參照物咯。
2： 二叉樹的類型
二叉樹中有兩種比較完美的類型，“完全二叉樹”和“滿二叉樹”。
1> 滿二叉樹
除葉子節(jié)點(diǎn)外，所有節(jié)點(diǎn)的度都為2，文章開頭處的樹就是這里的“滿二叉樹”。
2> 完全二叉樹
必須要滿足兩個(gè)條件就即可： 干掉最后一層，二叉樹變?yōu)椤皾M二叉樹”。
最后一層的葉節(jié)點(diǎn)必須是“從左到右”依次排開。
我們干掉文章開頭處的節(jié)點(diǎn)“F和”G",此時(shí)還是“完全二叉樹”，但已經(jīng)不是“滿二叉樹”了，你懂的。
3： 二叉樹的性質(zhì)
二叉樹中有5點(diǎn)性質(zhì)非常重要，也是俺們必須要記住的。
1> 二叉樹中，第i層的節(jié)點(diǎn)最多有2(i-1)個(gè)。
2> 深度為k的二叉樹最多有2k-1個(gè)節(jié)點(diǎn)。
3> 二叉樹中，葉子節(jié)點(diǎn)樹為N1個(gè)，度為2的節(jié)點(diǎn)有N2個(gè)，那么N1=N2+1。
4> 具有N個(gè)結(jié)點(diǎn)的二叉樹深度為（Log2 N）+1層。
5> N個(gè)結(jié)點(diǎn)的完全二叉樹如何用順序存儲(chǔ)，對(duì)于其中的一個(gè)結(jié)點(diǎn)i，存在以下關(guān)系，
2*i是結(jié)點(diǎn)i的父結(jié)點(diǎn)。
i/2是結(jié)點(diǎn)i的左孩子。
(i/2)+1是結(jié)點(diǎn)i的右孩子。
4： 二叉樹的順序存儲(chǔ)
同樣的存儲(chǔ)方式也有兩種，“順序存儲(chǔ)”和“鏈?zhǔn)酱鎯?chǔ)”。
1> 順序存儲(chǔ)
說實(shí)話，樹的存儲(chǔ)用順序結(jié)構(gòu)比較少，因?yàn)閺男再|(zhì)定理中我們都可以看出只限定為“完全二叉樹”，那么如果二叉樹不是
“完全二叉樹”，那我們就麻煩了，必須將其轉(zhuǎn)化為“完全二叉樹”，將空的節(jié)點(diǎn)可以用“#”代替，圖中也可看出，為了維護(hù)
性質(zhì)定理5的要求，我們犧牲了兩個(gè)”資源“的空間。
2> 鏈?zhǔn)酱鎯?chǔ)
上面也說了，順序存儲(chǔ)會(huì)造成資源的浪費(fèi)，所以嘛，我們開發(fā)中用的比較多的還是“鏈?zhǔn)酱鎯?chǔ)”，同樣“鏈?zhǔn)酱鎯?chǔ)”
也非常的形象，非常的合理。
一個(gè)結(jié)點(diǎn)存放著一個(gè)“左指針”和一個(gè)“右指針”，這就是二叉鏈表。
如何方便的查找到該結(jié)點(diǎn)的父結(jié)點(diǎn)，可以采用三叉鏈表。
5: 常用操作
一般也就是“添加結(jié)點(diǎn)“，“查找節(jié)點(diǎn)”，“計(jì)算深度”，“遍歷結(jié)點(diǎn)”，“清空結(jié)點(diǎn)”
1> 這里我們就用二叉鏈表來定義鏈?zhǔn)酱鎯?chǔ)模型
復(fù)制代碼 代碼如下:
#region 二叉鏈表存儲(chǔ)結(jié)構(gòu)
/// summary>
/// 二叉鏈表存儲(chǔ)結(jié)構(gòu)
/// /summary>
/// typeparam name="T">/typeparam>
public class ChainTreeT>
{
public T data;
public ChainTreeT> left;
public ChainTreeT> right;
}
#endregion
2> 添加結(jié)點(diǎn)
要添加結(jié)點(diǎn)，我們就要找到添加結(jié)點(diǎn)的父結(jié)點(diǎn)，并且根據(jù)指示插入到父結(jié)點(diǎn)中指定左結(jié)點(diǎn)或者右結(jié)點(diǎn)。
復(fù)制代碼 代碼如下:
#region 將指定節(jié)點(diǎn)插入到二叉樹中
/// summary>
/// 將指定節(jié)點(diǎn)插入到二叉樹中
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="node">/param>
/// param name="direction">插入做左是右/param>
/// returns>/returns>
public ChainTreeT> BinTreeAddNodeT>(ChainTreeT> tree, ChainTreeT> node, T data, Direction direction)
{
if (tree == null)
return null;
if (tree.data.Equals(data))
{
switch (direction)
{
case Direction.Left:
if (tree.left != null)
throw new Exception("樹的左節(jié)點(diǎn)不為空，不能插入");
else
tree.left = node;
break;
case Direction.Right:
if (tree.right != null)
throw new Exception("樹的右節(jié)點(diǎn)不為空，不能插入");
else
tree.right = node;
break;
}
}
BinTreeAddNode(tree.left, node, data, direction);
BinTreeAddNode(tree.right, node, data, direction);
return tree;
}
#endregion
3> 查找節(jié)點(diǎn)
二叉樹中到處都散發(fā)著遞歸思想，很能鍛煉一下我們對(duì)遞歸的認(rèn)識(shí)，同樣查找也是用到了遞歸思想。
復(fù)制代碼 代碼如下:
#region 在二叉樹中查找指定的key
/// summary>
///在二叉樹中查找指定的key
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="data">/param>
/// returns>/returns>
public ChainTreeT> BinTreeFindT>(ChainTreeT> tree, T data)
{
if (tree == null)
return null;
if (tree.data.Equals(data))
return tree;
return BinTreeFind(tree, data);
}
#endregion
4> 計(jì)算深度
這個(gè)問題糾結(jié)了我二個(gè)多小時(shí)，原因在于沒有深刻的體會(huì)到遞歸，其實(shí)主要思想就是遞歸左子樹和右子樹，然后得出較大的一個(gè)。
復(fù)制代碼 代碼如下:
#region 獲取二叉樹的深度
/// summary>
/// 獲取二叉樹的深度
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// returns>/returns>
public int BinTreeLenT>(ChainTreeT> tree)
{
int leftLength;
int rightLength;
if (tree == null)
return 0;
//遞歸左子樹的深度
leftLength = BinTreeLen(tree.left);
//遞歸右子書的深度
rightLength = BinTreeLen(tree.right);
if (leftLength > rightLength)
return leftLength + 1;
else
return rightLength + 1;
}
#endregion
5> 遍歷結(jié)點(diǎn)
二叉樹中遍歷節(jié)點(diǎn)的方法還是比較多的，有“先序”，“中序”，“后序”，“按層”，其實(shí)這些東西只可意會(huì)，不可言傳，真的很難在口頭
上說清楚，需要反復(fù)的體會(huì)遞歸思想。
先序：先訪問根，然后遞歸訪問左子樹，最后遞歸右子樹。（DLR模式）
中序：先遞歸訪問左子樹，在訪問根，最后遞歸右子樹。（LDR模式）
后序：先遞歸訪問左子樹，然后遞歸訪問右子樹，最后訪問根。（LRD模式）
按層：這個(gè)比較簡單，從上到下，從左到右的遍歷節(jié)點(diǎn)。
復(fù)制代碼 代碼如下:
#region 二叉樹的先序遍歷
/// summary>
/// 二叉樹的先序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_DLRT>(ChainTreeT> tree)
{
if (tree == null)
return;
//先輸出根元素
Console.Write(tree.data + "\t");
//然后遍歷左子樹
BinTree_DLR(tree.left);
//最后遍歷右子樹
BinTree_DLR(tree.right);
}
#endregion
#region 二叉樹的中序遍歷
/// summary>
/// 二叉樹的中序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LDRT>(ChainTreeT> tree)
{
if (tree == null)
return;
//優(yōu)先遍歷左子樹
BinTree_LDR(tree.left);
//然后輸出節(jié)點(diǎn)
Console.Write(tree.data + "\t");
//最后遍歷右子樹
BinTree_LDR(tree.right);
}
#endregion
#region 二叉樹的后序遍歷
/// summary>
/// 二叉樹的后序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LRDT>(ChainTreeT> tree)
{
if (tree == null)
return;
//優(yōu)先遍歷左子樹
BinTree_LRD(tree.left);
//然后遍歷右子樹
BinTree_LRD(tree.right);
//最后輸出節(jié)點(diǎn)元素
Console.Write(tree.data + "\t");
}
#endregion
#region 二叉樹的按層遍歷
/// summary>
/// 二叉樹的按層遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LevelT>(ChainTreeT> tree)
{
if (tree == null)
return;
//申請(qǐng)保存空間
ChainTreeT>[] treeList = new ChainTreeT>[Length];
int head = 0;
int tail = 0;
//存放數(shù)組
treeList[tail] = tree;
//循環(huán)鏈中計(jì)算tail位置
tail = (tail + 1) % Length;
while (head != tail)
{
var tempNode = treeList[head];
head = (head + 1) % Length;
//輸出節(jié)點(diǎn)
Console.Write(tempNode.data + "\t");
//如果左子樹不為空,則將左子樹存于數(shù)組的tail位置
if (tempNode.left != null)
{
treeList[tail] = tempNode.left;
tail = (tail + 1) % Length;
}
//如果右子樹不為空，則將右子樹存于數(shù)組的tail位置
if (tempNode.right != null)
{
treeList[tail] = tempNode.right;
tail = (tail + 1) % Length;
}
}
}
#endregion
6> 清空二叉樹
雖然C#里面有GC，但是我們能自己釋放的就不麻煩GC了，同樣清空二叉樹節(jié)點(diǎn)，我們用到了遞歸，說實(shí)話，這次練習(xí)讓我喜歡
上的遞歸，雖然XXX的情況下，遞歸的不是很好，但是遞歸還是很強(qiáng)大的。
復(fù)制代碼 代碼如下:
#region 清空二叉樹
/// summary>
/// 清空二叉樹
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTreeClearT>(ChainTreeT> tree)
{
//遞的結(jié)束點(diǎn)，歸的起始點(diǎn)
if (tree == null)
return;
BinTreeClear(tree.left);
BinTreeClear(tree.right);
//在歸的過程中，釋放當(dāng)前節(jié)點(diǎn)的數(shù)據(jù)空間
tree = null;
}
#endregion
最后上一下總的代碼
復(fù)制代碼 代碼如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace ChainTree
{
public class Program
{
static void Main(string[] args)
{
ChainTreeManager manager = new ChainTreeManager();
//插入節(jié)點(diǎn)操作
ChainTreestring> tree = CreateRoot();
//插入節(jié)點(diǎn)數(shù)據(jù)
AddNode(tree);
//先序遍歷
Console.WriteLine("\n先序結(jié)果為： \n");
manager.BinTree_DLR(tree);
//中序遍歷
Console.WriteLine("\n中序結(jié)果為： \n");
manager.BinTree_LDR(tree);
//后序遍歷
Console.WriteLine("\n后序結(jié)果為： \n");
manager.BinTree_LRD(tree);
//層次遍歷
Console.WriteLine("\n層次結(jié)果為： \n");
manager.Length = 100;
manager.BinTree_Level(tree);
Console.WriteLine("\n樹的深度為：" + manager.BinTreeLen(tree) + "\n");
Console.ReadLine();
}
#region 生成根節(jié)點(diǎn)
/// summary>
/// 生成根節(jié)點(diǎn)
/// /summary>
/// returns>/returns>
static ChainTreestring> CreateRoot()
{
ChainTreestring> tree = new ChainTreestring>();
Console.WriteLine("請(qǐng)輸入根節(jié)點(diǎn)，方便我們生成樹\n");
tree.data = Console.ReadLine();
Console.WriteLine("根節(jié)點(diǎn)生成已經(jīng)生成\n");
return tree;
}
#endregion
#region 插入節(jié)點(diǎn)操作
/// summary>
/// 插入節(jié)點(diǎn)操作
/// /summary>
/// param name="tree">/param>
static ChainTreestring> AddNode(ChainTreestring> tree)
{
ChainTreeManager mananger = new ChainTreeManager();
while (true)
{
ChainTreestring> node = new ChainTreestring>();
Console.WriteLine("請(qǐng)輸入要插入節(jié)點(diǎn)的數(shù)據(jù)：\n");
node.data = Console.ReadLine();
Console.WriteLine("請(qǐng)輸入要查找的父節(jié)點(diǎn)數(shù)據(jù)：\n");
var parentData = Console.ReadLine();
if (tree == null)
{
Console.WriteLine("未找到您輸入的父節(jié)點(diǎn)，請(qǐng)重新輸入。");
continue;
}
Console.WriteLine("請(qǐng)確定要插入到父節(jié)點(diǎn)的：1 左側(cè)，2 右側(cè)");
Direction direction = (Direction)Enum.Parse(typeof(Direction), Console.ReadLine());
tree = mananger.BinTreeAddNode(tree, node, parentData, direction);
Console.WriteLine("插入成功，是否繼續(xù)？ 1 繼續(xù)， 2 退出");
if (int.Parse(Console.ReadLine()) == 1)
continue;
else
break;
}
return tree;
}
#endregion
}
#region 插入左節(jié)點(diǎn)或者右節(jié)點(diǎn)
/// summary>
/// 插入左節(jié)點(diǎn)或者右節(jié)點(diǎn)
/// /summary>
public enum Direction { Left = 1, Right = 2 }
#endregion
#region 二叉鏈表存儲(chǔ)結(jié)構(gòu)
/// summary>
/// 二叉鏈表存儲(chǔ)結(jié)構(gòu)
/// /summary>
/// typeparam name="T">/typeparam>
public class ChainTreeT>
{
public T data;
public ChainTreeT> left;
public ChainTreeT> right;
}
#endregion
/// summary>
/// 二叉樹的操作幫助類
/// /summary>
public class ChainTreeManager
{
#region 按層遍歷的Length空間存儲(chǔ)
/// summary>
/// 按層遍歷的Length空間存儲(chǔ)
/// /summary>
public int Length { get; set; }
#endregion
#region 將指定節(jié)點(diǎn)插入到二叉樹中
/// summary>
/// 將指定節(jié)點(diǎn)插入到二叉樹中
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="node">/param>
/// param name="direction">插入做左是右/param>
/// returns>/returns>
public ChainTreeT> BinTreeAddNodeT>(ChainTreeT> tree, ChainTreeT> node, T data, Direction direction)
{
if (tree == null)
return null;
if (tree.data.Equals(data))
{
switch (direction)
{
case Direction.Left:
if (tree.left != null)
throw new Exception("樹的左節(jié)點(diǎn)不為空，不能插入");
else
tree.left = node;
break;
case Direction.Right:
if (tree.right != null)
throw new Exception("樹的右節(jié)點(diǎn)不為空，不能插入");
else
tree.right = node;
break;
}
}
BinTreeAddNode(tree.left, node, data, direction);
BinTreeAddNode(tree.right, node, data, direction);
return tree;
}
#endregion
#region 獲取二叉樹指定孩子的狀態(tài)
/// summary>
/// 獲取二叉樹指定孩子的狀態(tài)
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="direction">/param>
/// returns>/returns>
public ChainTreeT> BinTreeChildT>(ChainTreeT> tree, Direction direction)
{
ChainTreeT> childNode = null;
if (tree == null)
throw new Exception("二叉樹為空");
switch (direction)
{
case Direction.Left:
childNode = tree.left;
break;
case Direction.Right:
childNode = tree.right;
break;
}
return childNode;
}
#endregion
#region 獲取二叉樹的深度
/// summary>
/// 獲取二叉樹的深度
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// returns>/returns>
public int BinTreeLenT>(ChainTreeT> tree)
{
int leftLength;
int rightLength;
if (tree == null)
return 0;
//遞歸左子樹的深度
leftLength = BinTreeLen(tree.left);
//遞歸右子書的深度
rightLength = BinTreeLen(tree.right);
if (leftLength > rightLength)
return leftLength + 1;
else
return rightLength + 1;
}
#endregion
#region 判斷二叉樹是否為空
/// summary>
/// 判斷二叉樹是否為空
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// returns>/returns>
public bool BinTreeisEmptyT>(ChainTreeT> tree)
{
return tree == null ? true : false;
}
#endregion
#region 在二叉樹中查找指定的key
/// summary>
///在二叉樹中查找指定的key
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
/// param name="data">/param>
/// returns>/returns>
public ChainTreeT> BinTreeFindT>(ChainTreeT> tree, T data)
{
if (tree == null)
return null;
if (tree.data.Equals(data))
return tree;
return BinTreeFind(tree, data);
}
#endregion
#region 清空二叉樹
/// summary>
/// 清空二叉樹
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTreeClearT>(ChainTreeT> tree)
{
//遞的結(jié)束點(diǎn)，歸的起始點(diǎn)
if (tree == null)
return;
BinTreeClear(tree.left);
BinTreeClear(tree.right);
//在歸的過程中，釋放當(dāng)前節(jié)點(diǎn)的數(shù)據(jù)空間
tree = null;
}
#endregion
#region 二叉樹的先序遍歷
/// summary>
/// 二叉樹的先序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_DLRT>(ChainTreeT> tree)
{
if (tree == null)
return;
//先輸出根元素
Console.Write(tree.data + "\t");
//然后遍歷左子樹
BinTree_DLR(tree.left);
//最后遍歷右子樹
BinTree_DLR(tree.right);
}
#endregion
#region 二叉樹的中序遍歷
/// summary>
/// 二叉樹的中序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LDRT>(ChainTreeT> tree)
{
if (tree == null)
return;
//優(yōu)先遍歷左子樹
BinTree_LDR(tree.left);
//然后輸出節(jié)點(diǎn)
Console.Write(tree.data + "\t");
//最后遍歷右子樹
BinTree_LDR(tree.right);
}
#endregion
#region 二叉樹的后序遍歷
/// summary>
/// 二叉樹的后序遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LRDT>(ChainTreeT> tree)
{
if (tree == null)
return;
//優(yōu)先遍歷左子樹
BinTree_LRD(tree.left);
//然后遍歷右子樹
BinTree_LRD(tree.right);
//最后輸出節(jié)點(diǎn)元素
Console.Write(tree.data + "\t");
}
#endregion
#region 二叉樹的按層遍歷
/// summary>
/// 二叉樹的按層遍歷
/// /summary>
/// typeparam name="T">/typeparam>
/// param name="tree">/param>
public void BinTree_LevelT>(ChainTreeT> tree)
{
if (tree == null)
return;
//申請(qǐng)保存空間
ChainTreeT>[] treeList = new ChainTreeT>[Length];
int head = 0;
int tail = 0;
//存放數(shù)組
treeList[tail] = tree;
//循環(huán)鏈中計(jì)算tail位置
tail = (tail + 1) % Length;
while (head != tail)
{
var tempNode = treeList[head];
head = (head + 1) % Length;
//輸出節(jié)點(diǎn)
Console.Write(tempNode.data + "\t");
//如果左子樹不為空,則將左子樹存于數(shù)組的tail位置
if (tempNode.left != null)
{
treeList[tail] = tempNode.left;
tail = (tail + 1) % Length;
}
//如果右子樹不為空，則將右子樹存于數(shù)組的tail位置
if (tempNode.right != null)
{
treeList[tail] = tempNode.right;
tail = (tail + 1) % Length;
}
}
}
#endregion
}
}
我們把文章開頭的“二叉樹”的節(jié)點(diǎn)輸入到我們的結(jié)構(gòu)中，看看遍歷效果咋樣。
您可能感興趣的文章:- 算法系列15天速成 第十四天 圖【上】
- 算法系列15天速成——第十三天 樹操作【下】
- 算法系列15天速成 第十二天 樹操作【中】
- 算法系列15天速成 第十天 棧
- 算法系列15天速成 第八天 線性表【下】
- 算法系列15天速成 第九天 隊(duì)列
- 算法系列15天速成 第七天 線性表【上】
- 算法系列15天速成 第六天 五大經(jīng)典查找【下】
- 算法系列15天速成 第五天 五大經(jīng)典查找【中】
- 算法系列15天速成 第四天 五大經(jīng)典查找【上】
- 算法系列15天速成 第三天 七大經(jīng)典排序【下】
- 算法系列15天速成 第二天 七大經(jīng)典排序【中】
- 算法系列15天速成 第一天 七大經(jīng)典排序【上】
- 算法系列15天速成——第十五天 圖【下】（大結(jié)局）
