目錄
- 一、理解廣度優先算法
- 1.1、分析如何進行廣度優先探索
- 1.2���、我們來總結一下
- 1.3、代碼分析
- 二、代碼實現廣度優先算法走迷宮
一�����、理解廣度優先算法
我們要實現的是廣度優先算法走迷宮
比如,我們有一個下面這樣的迷宮
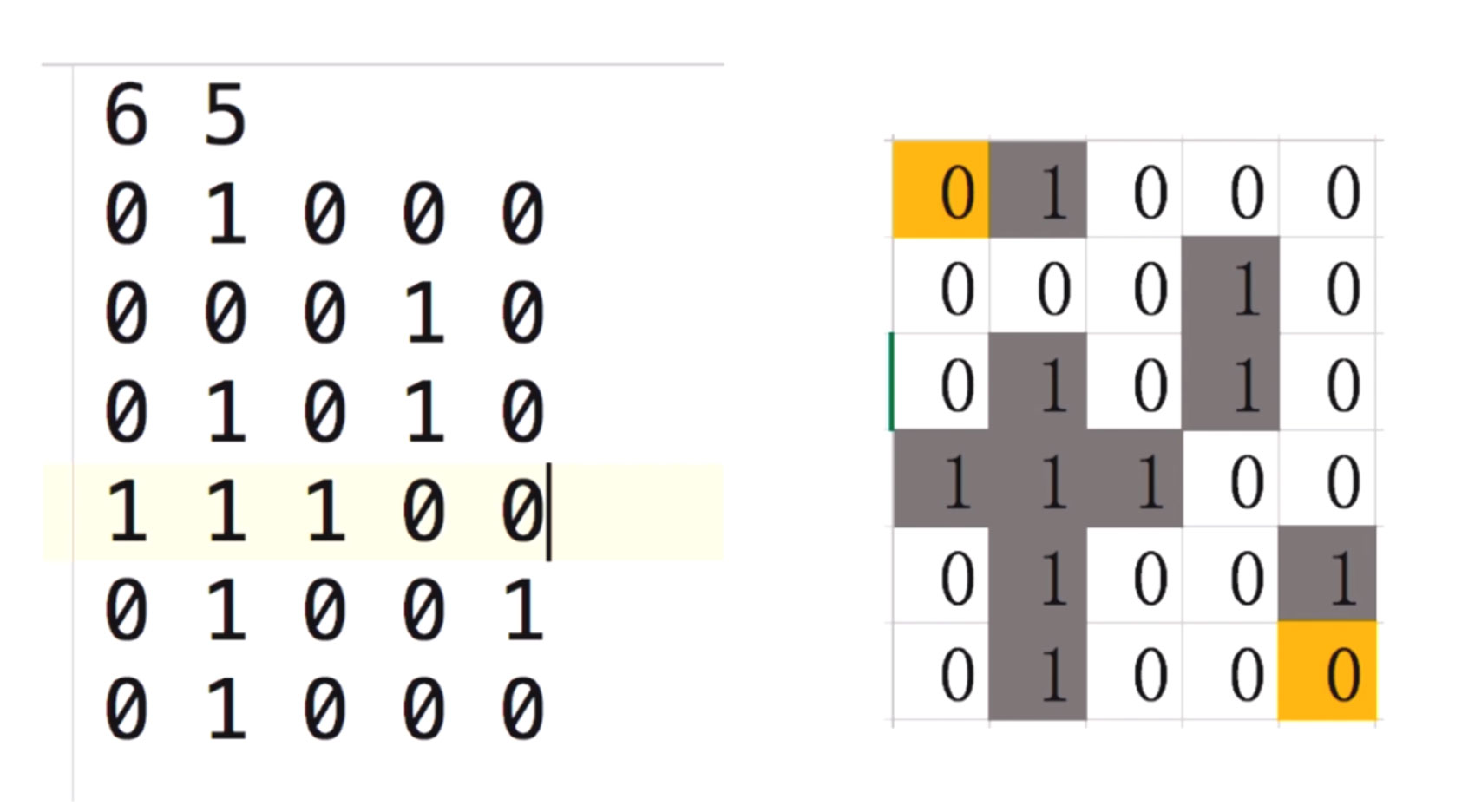
這個迷宮是6行5列
其中0代表可以走的路, 1代表一堵墻. 我們把墻標上言責, 就如右圖所示. 其中(0,0)是起點, (6, 5)是終點.
我們要做的是, 從起點走到終點最近的路徑.
這個例子是拋轉隱喻, 介紹廣度優先算法, 廣度優先算法的應用很廣泛, 所以, 先來看看規律
1.1���、分析如何進行廣度優先探索
第一步, 我們先明確起點. 這個起點有上下左右四個方向可以探索. 我們按照順時針順序探索, 上 左 下 右

第二步: 起始位置向外探索, 有4個方向.

如上圖紅色標出的位置. 也就是起始位置可以向外探索的路徑有4個. 上 左 下 右
我們再來繼續探索.
第三步: 再次明確探索方向是 上 左 下 右
第四步: 探索上方的紅1, 上方的紅1可以向外探索的路徑有3個

第五步: 探索左側紅1, 左側紅1 有兩條路徑向外探索,
為什么是兩個呢? 本來是有3個, 但上面的路徑已經被上面的紅1探索過了, 所以, 不重復探索的原則, 左側紅1 向外擴展的路徑有2條

第六步: 下面的紅1 向外探索的路徑有2條

第七步: 右側的紅1向外探索的路徑, 如上圖可見, 只剩下1條了

第二輪探索, 得到的探索結果是:

經過第二輪探索, 一共探索出了8條路徑, 也就是8個黑2
接下來進行第三輪探索. 順序依然是順時針方向,
1. 第一個2向外探索的路徑有3條

2. 第二個黑2向外探索的路徑只有1條
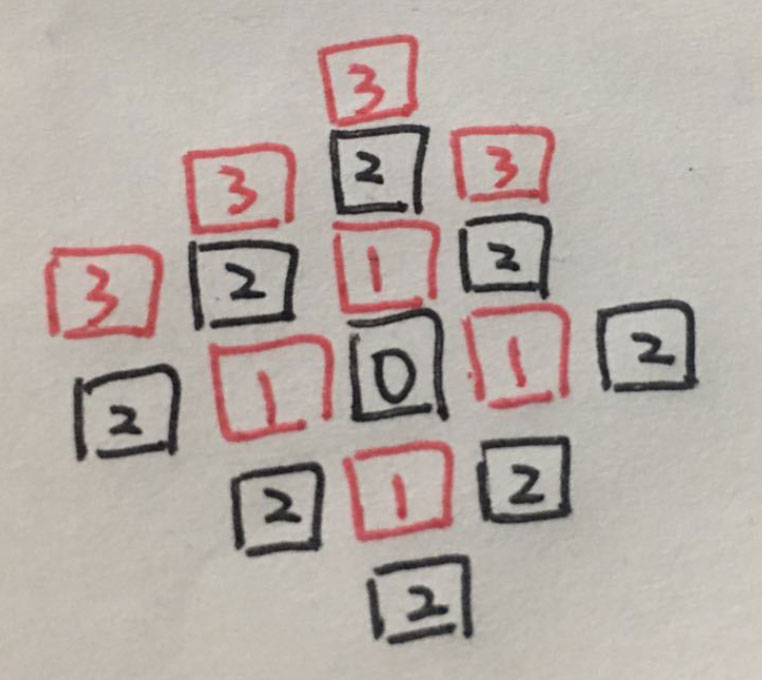
3. 第三個黑2向外探索的路徑有2條

4. 第四個黑2向外探索的路徑有1條

5. 第五個黑2 向外探索的路徑有兩條

6. 第六個黑2向外探索的路徑有1條

7. 第七個黑2向外探索的路徑有兩條

8. 第8個黑2向外探索的路徑為0條. 已經沒有路徑. 所以不再向外探索
通過第三輪向外探索, 我們探索出來了12條路徑.
這是有的節點可以向外探索3條路徑,有的可以向外探索2條路徑, 有的向外探索1條路徑, 有的沒有路徑可以向外探索了.
總結:
通過上面的例子, 我們可以看到每個節點的3中狀態. 我們來分析一下, 有哪三種狀態.
剛開始, 只有一個其實位置0. 這個0是已知的, 還沒有開始向外探索. 外面還有好多等待探索的節點.所以,此時的0, 是已經發現還未探索的節點
當0開始向外探索, 探索到4個1, 這時候0就變成了已經發現且已經探索的節點. 二1變成了一經發現還未探索的節點. 其實此時外面還有3, 4, 5 這些還未被發現未被探索的節點.
我們通過分析, 廣度優先算法還有一個特點, 那就是循環遍歷, 第一輪的紅1都探索完了, 在進行黑2的探索, 不會說紅1探索出來一個, 還沒有全部完成,就繼續向外探索.
總結規律如下:
1. 節點有三種狀態
- a. 已經發現還未探索的節點
- b. 已經發現并且已經探索的節點
- c. 還未發現且未探索的節點
2. 階段探索的順序
按照每一輪全部探索完,在探索下一輪, 這樣就形成了一個隊列, 我們把已經發現還未探索的節點放到隊列里
接下來我們開始探索了.
首先, 我們知道迷宮的起始位置, (0,0)點. 當前我們站在起始位置(0,0), 那么這個起點就是已經發現還未探索的節點.
我們定義一個隊列來存放已經發現但還未探索的節點
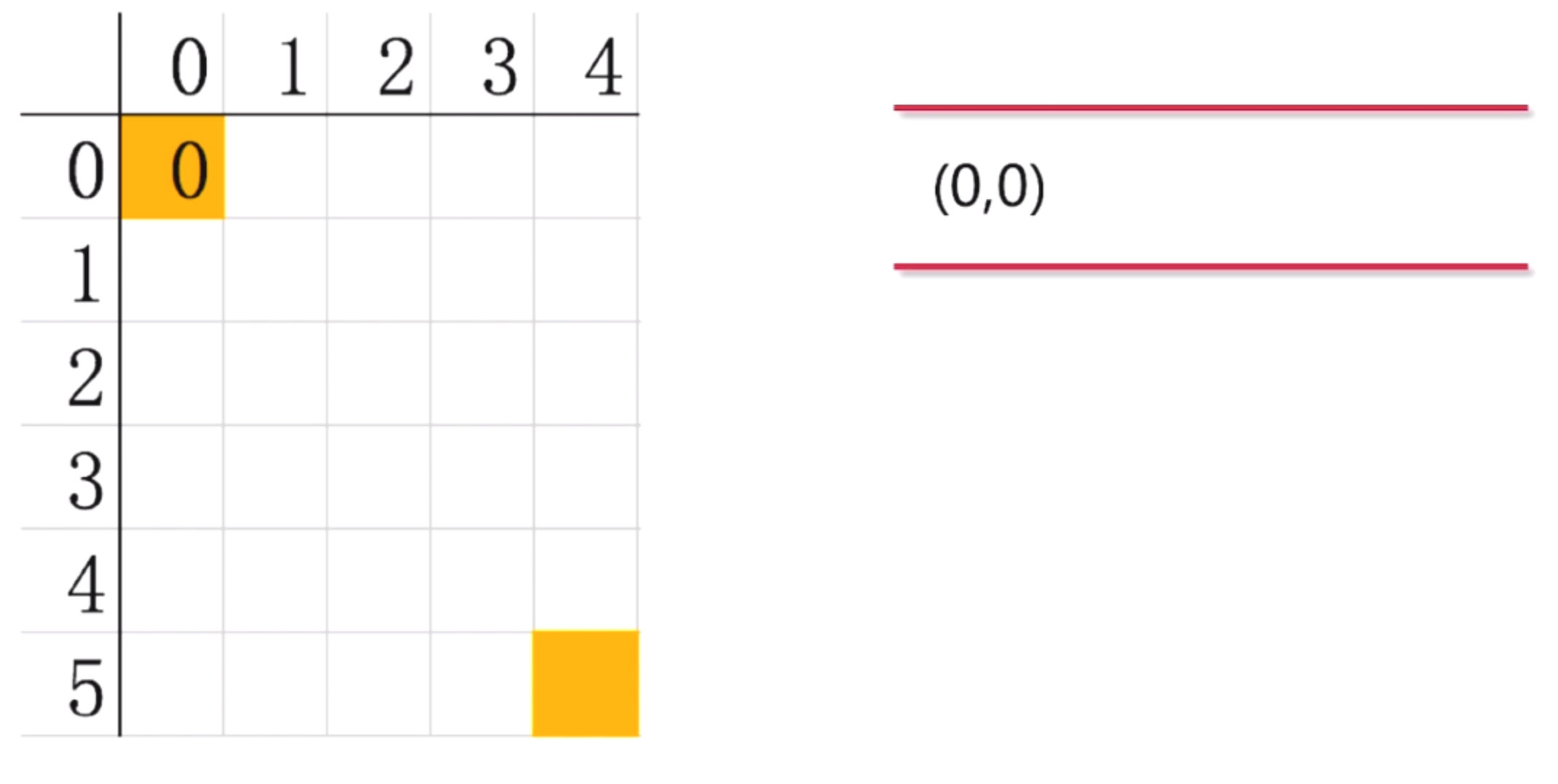
第二步: 從隊列中取出節點(0,0), 開始下一步探索.我們看看迷宮最終的樣子

我們看到(0,0)只能向下走, 他的右邊是一堵墻, 走不了. 上面,左面也不能走. 所以, 探索出來的路徑只有一個(1,0), 吧(1,0)放入到隊列中
第三步: 我們在從隊列中把(1,0)取出來進行探索, 這時隊列就空了.
對照迷宮, (1,0)可以向下走, 可以向右走. 不能向上和向左. 因此, (1,0)探索出來兩條路, (2,0) 和(1,1), 把這兩個點放入到隊列中
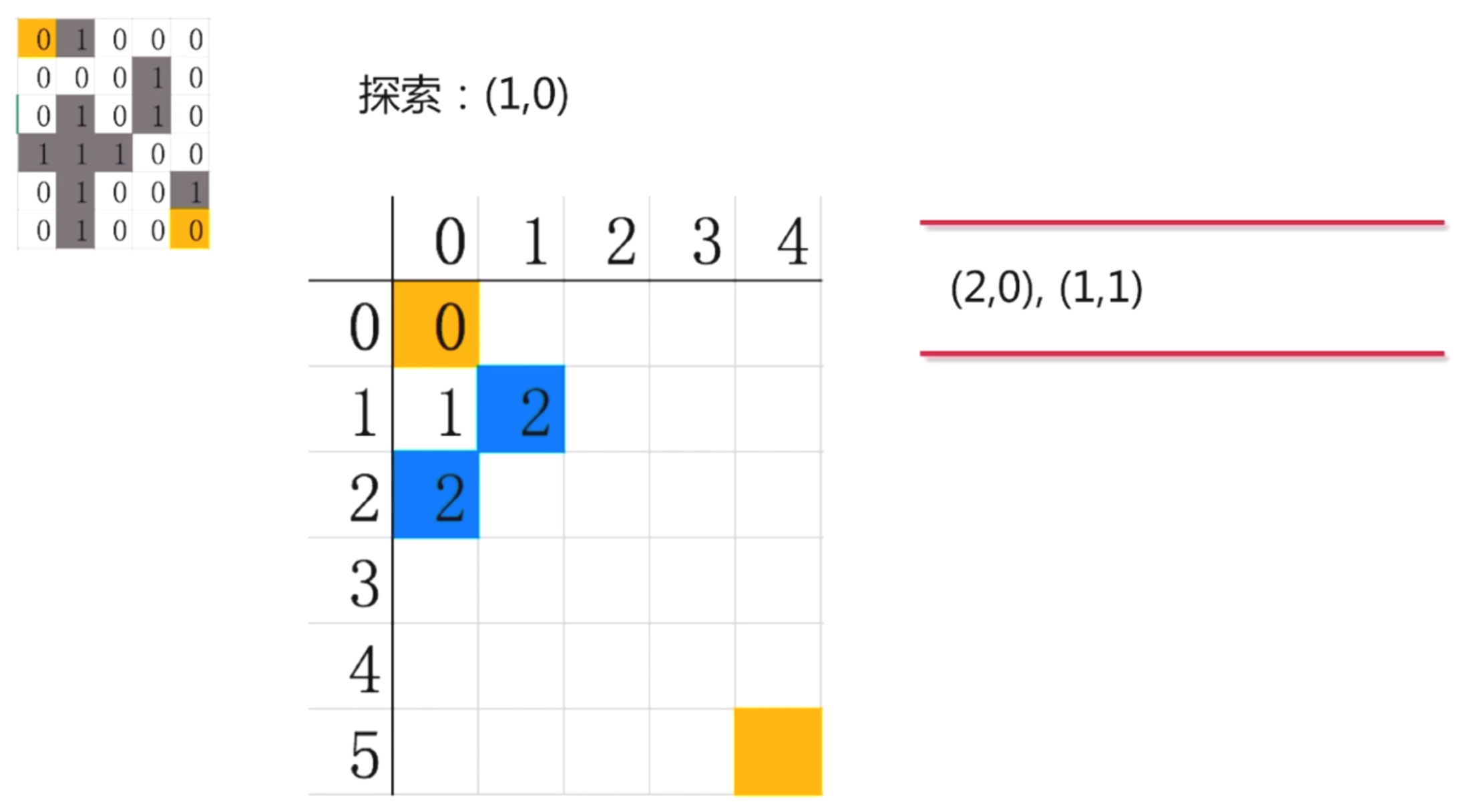
第四步: 接下來我們來探索(2,0)這個點, 對照迷宮, 我沒發現(2,0)這個點下和右都是墻, 左不能走, 上就走回去了也不可以. 所以, (2,0)是個死路, 探索出來的路徑是0
第五步: 繼續探索(1,1), 對照迷宮, (1,1)只能向右探索到(1,2) , 因此我們把(1,2)放入隊列中
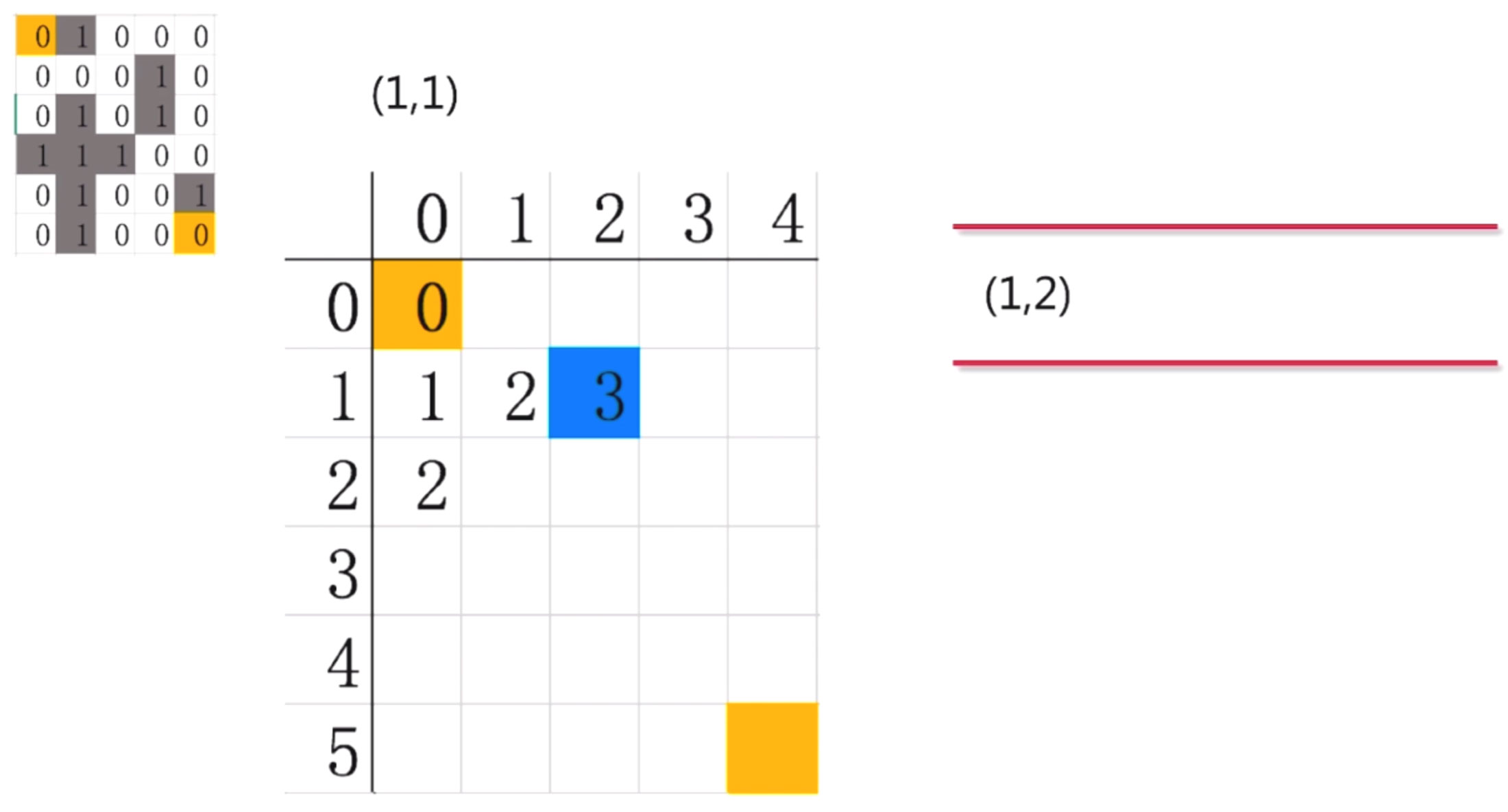
第六步:對(1,2)繼續探索, 發現有兩條路徑可以走(2,2)和(0,2), 然后, 將這兩個點放到隊列中
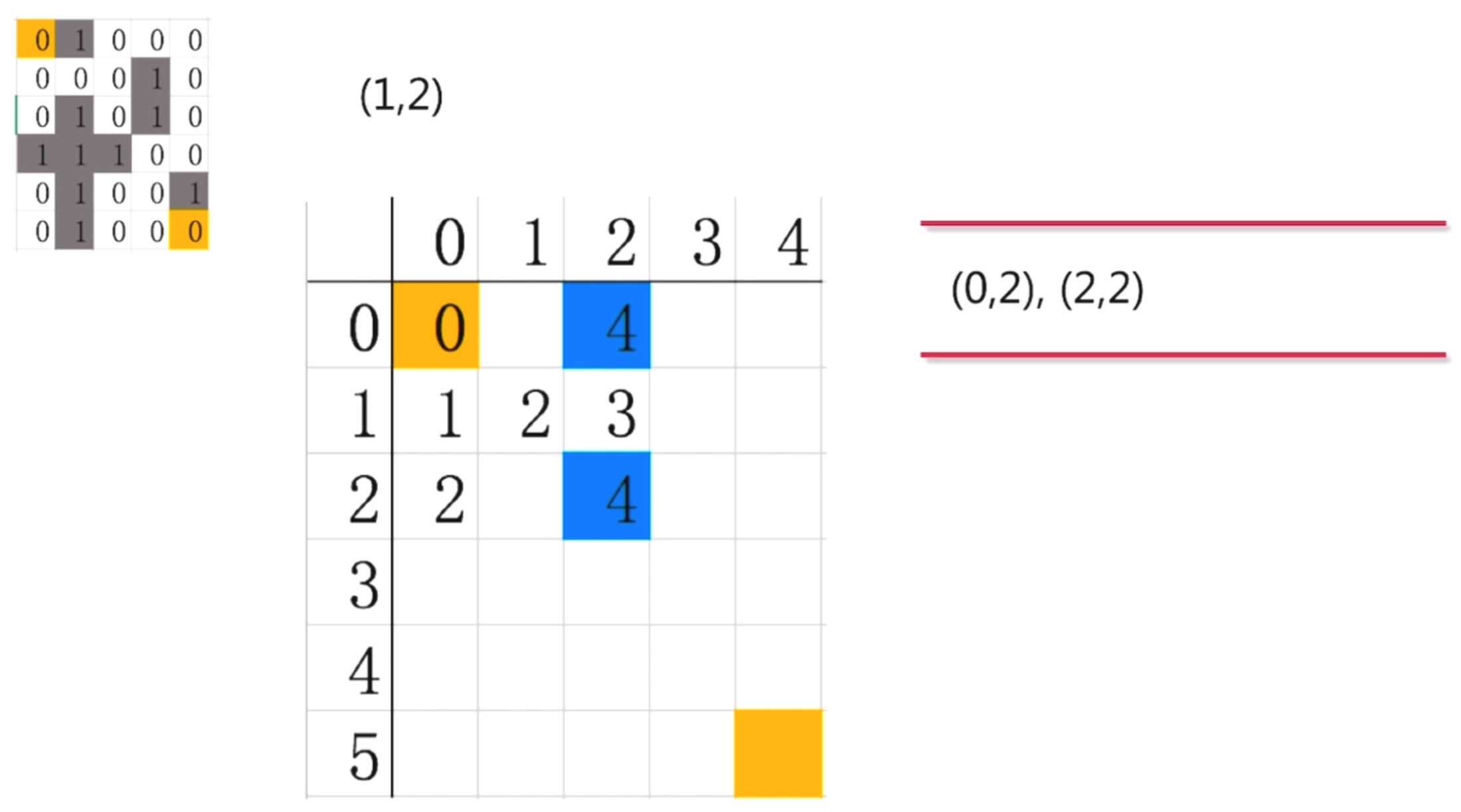
第七步: 接下來繼續這樣探索下去, 一直走一直走, 走到最后就是這樣的
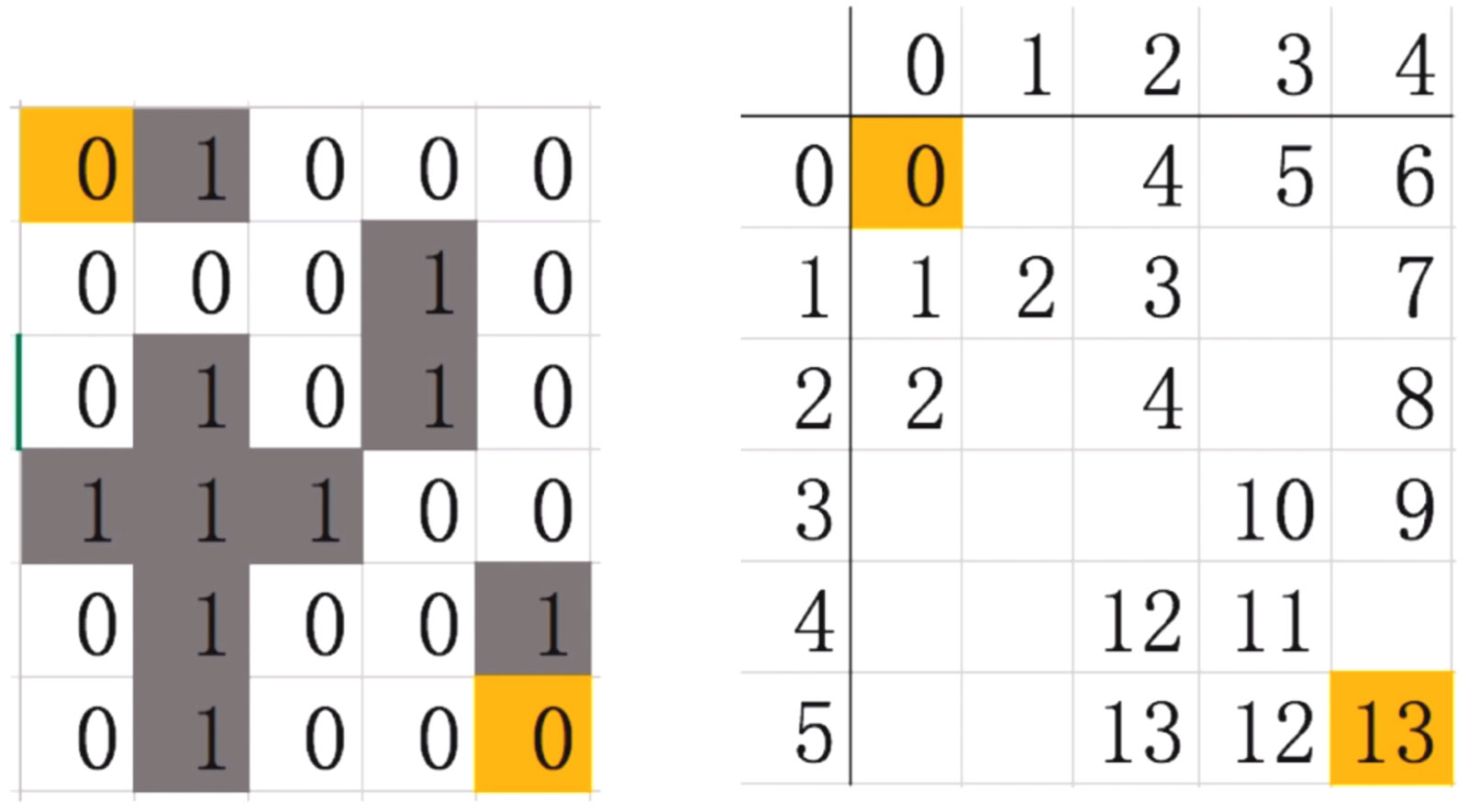
那我們要怎么來判斷路徑呢? 倒過來走, 從13開始, 上一個數12, 只有一個, 12上面只有一個數是11, 只有一個, 一次類推, 一直找到1, 找到0.
第八步: 廣度優先算法, 什么時候結束呢? 兩種情況
- 第一種: 走到最后13的位置
- 第二種: 死路, 走到一個位置, 不能再走了. 如何判斷呢?隊列中沒有可探索的點了, 探索結束
1.2�、我們來總結一下
1. 從(0,0)點開始, 將已經發現還未探索的點, 放入到隊列中.
2. 從隊列中取出已經發現還未探索的節點, 進行探索, 探索的方式是, 像四周探索, 然后把新發現還未探索的節點從隊列中取出來.
3. 如何判斷呢? 如果當前是一堵墻, 也就是他的value=0, 那么探索失敗. 向左探索的時候, 如果左邊是(0,*)探索失敗. 向上探索的時候, 如果上面是(*,0)探索失敗; 像右面探索的時候, 碰到邊(*,4)探索失敗. 向下探索, 碰到(5,*)探索失敗. 也就是, 橫向坐標的范圍是 0=x=4, 縱坐標是 0=y=5
4. 已經探索過的節點不要重復探索
1.3、代碼分析
1. 隊列可以用一個數組來實現. 先進先出
2. 點用二維數據來表示. 但是go中的二維數組的含義是一位數組里的值又是一個數組.比如[][]int, 他是一個一維數組[]int, 里面的值又是一個一維數組.[]int.
那么用在這里就是, 縱坐標表示有6行, 那么他是一個[6]int, 橫坐標表示每行里面又是一個數組, 每行有6個元素[5]int, 所以, 這就是一個[6][5]int 有6行5列的數組.
二�、代碼實現廣度優先算法走迷宮
第一步: step代表從start開始, 走了多少步走到目標點, 最后的路徑是通過這個創建出來的, 最后從后往前推就可以算出最短路徑
第二步: 定義一個隊列, 用來保存已經發現還未探索的點, 隊列里的初始值是(0,0)點
第三步: 開始走迷宮, 走迷宮退出的條件有兩個
1. 走到終點, 退出
2. 隊列中沒有元素, 退出
第四步: 判斷坐標是否符合探索的要求
1. maze at next is 0
2. and setp at next is 0, 如果step的值不是0 ,說明曾經到過這個點了, 不能重復走
3. next != start 處理特殊點, (0,0)點
第五步: 已經找到這個點了, 計算當前的步數, 并加入隊列中
package main
import (
"fmt"
"os"
)
func readFile(filename string) [][]int{
// 定義一個行和列,用來接收迷宮是幾行幾列的數組
var row, col int
file, e := os.Open(filename)
if e != nil {
panic("error")
}
defer file.Close()
fmt.Fscan(file, row, col)
// 定義一個數組
// 注意: 定義數組的時候, 我們只要傳入幾行就可以了.
// 二維數組的含義, 其實質是一個一維數組, 一維數組里每一個元素又是一個數組
maze := make([][]int, row)
for i := 0; i len(maze); i++ {
maze[i] = make([]int, col)
for j := 0; j len(maze[i]); j++ {
fmt.Fscan(file, maze[i][j])
}
}
return maze
}
type point struct {
i, j int
}
// 當前節點, 向四個方向探索后的節點
// 這里使用的是返回新的節點的方式, 不修改原來的節點. 所以使用的是值拷貝,而不是傳地址
func (p point) add(dir point) point{
return point{p.i + dir.i, p.j + dir.j }
}
// 獲取某個點的坐標值
// 同時判斷這個點有沒有越界, 返回的是這個值是否有效
// return 第一個參數表示返回的值是否是1, 是1表示撞墻了
// 第二個參數表示返回的值是否不越界, 不越界返回true, 越界,返回false 就和你
func (p point) at(grid [][]int) (int, bool) {
if p.i 0 || p.i >= len(grid) {
return 0, false
}
if p.j 0 || p.j >= len(grid[0]) {
return 0, false
}
return grid[p.i][p.j], true
}
// 定義要探索的方向, 上下左右四個方向
var dirs = []point {
point{-1, 0},
point{0, -1},
point{1, 0},
point{0, 1},
}
// 走迷宮
func walk(maze [][]int, start, end point) [][]int {
// 第一步: step代表從start開始, 走了多少步走到目標點, 最后的路徑是通過這個創建出來的, 最后從后往前推就可以算出最短路徑
// 2. 通step還可以知道哪些點是到過的, 哪些點是沒到過的
step := make([][]int, len(maze))
for i := range step {
// 定義每一行有多少列, 這樣就定義了一個和迷宮一樣的二維數組
step[i] = make([]int, len(maze[i]))
}
// 第二步: 定義一個隊列, 用來保存已經發現還未探索的點, 隊列里的初始值是(0,0)點
Que := []point{start}
// 第三步: 開始走迷宮, 走迷宮退出的條件有兩個
// 1. 走到終點, 退出
// 2. 隊列中沒有元素, 退出
for len(Que) > 0 {
// 開始探索, 依次取出隊列中, 已經發現還未探索的元素
// cur 表示當前要探索的節點
cur := Que[0]
// 然后從頭拿掉第一個元素
Que = Que[1:]
// 如果這個點是終點, 就不向下探索了
if cur == end {
break
}
// 當前節點怎么探索呢? 要往上下左右四個方向去探索
for _, dir := range dirs {
// 探索下一個節點, 這里獲取下一個節點的坐標. 當前節點+方向
next := cur.add(dir)
// 判斷坐標是否符合探索的要求
// 1. maze at next is 0
// 2. and setp at next is 0, 如果step的值不是0 ,說明曾經到過這個點了, 不能重復走
// 3. next != start 處理特殊點, (0,0)點
// 探索這個點是否是墻
val, ok := next.at(maze)
if !ok || val == 1 {
continue
}
// 探索這個點是否已經走過
val, ok = next.at(step)
if val != 0 || !ok {
continue
}
// 走到起始點了, 返回
if next == start {
continue
}
// 已經找到這個點了, 計算當前的步數
curval, _ := cur.at(step) // 當前這一步的步數
step[next.i][next.j] = curval + 1 // 下一步是當前步數+1
Que = append(Que, next) // 將下一步節點放入到隊列中
}
}
return step
}
func main() {
maze := readFile("maze/maze.in")
steps := walk(maze, point{0, 0}, point{len(maze) - 1, len(maze[0]) - 1})
// len(maze)-1, len[maze[0]]-1 是終點
// 0,0是起始點
for _, row := range steps {
for _, val := range row {
fmt.Printf("%3d", val)
}
fmt.Println()
}
}
以上就是詳解Go語言運用廣度優先搜索走迷宮的詳細內容�,更多關于Go 廣度優先搜索走迷宮的資料請關注腳本之家其它相關文章�����!
您可能感興趣的文章:- Go語言實現的樹形結構數據比較算法實例
- Go語言算法之尋找數組第二大元素的方法
- Golang算法問題之數組按指定規則排序的方法分析
- Golang排列組合算法問題之全排列實現方法